Squeezing the Numbers to Design a Weaving Draft

When mathematicians become interested in weaving, the first thing they turn to are ways to express weaving design using the tools they already know so well.  It works in reverse too.  Weavers start using numerical sequences, algebraic equations and more to make their weaving more interesting and give it a new dimension. 

The first mathematical sequence I learned to use in weaving (well, in knitting too) was a stripe generator called the Fibonnaci Sequence.  For years, I used the first numbers in the sequence, not even thinking that maybe I only needed to use just a portion to make interesting designs.  Instead of starting with 0,1,1,1,2,3  maybe I could cut to 3,5,8,13 or just leave it at 3.5.8.  It really only occurred to me recently that I didn't need to reserve the sequence for stripes - it could be also used for profile drafts.  3 - 5 - 8.  Reverse it for a symmetry, add color and you have a fine piece to work from. Another trick to change the look of this profile - change the tie up box and see what happens.



 

When you start looking for these ideas, they seem to just pop out of the woodwork.  I was taking a trip around my Handwoven magazine collection, seeing what I could find in the way of interesting designs for towels.  I ran across an article in Jan/Feb 1998 called Algebraic Expressions:  Design for Weaving written by Lana Schneider. She described a method of design developed by a math teacher called Ada K. Dietz in 1946.  Ada used algebraic equations to create profile drafts, color sequences and even thread by thread sequences for weaving.  Wouldn't it be wonderful if I could actually read Ada's work?  Turns out, the PDF file is available from the Handweaving.net and it's a free download.

 

Well, this was just too good to be true.  It seems Ada instinctively knew that many of us had forgotten what we once knew about the square or cube of a binomial.  She spelled it out for us and gave us some examples showing how she used (a + b)²  The breakdown is in her article, so you don't need to sweat out her procedure all by yourself.  The Handwoven article is nice and tidy and easier to read, so if you have access to that, use it.

 

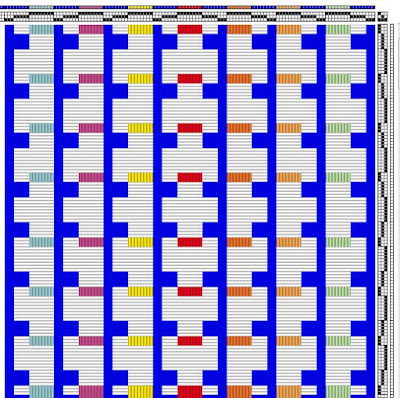
After reading the document about Ada's work, I jotted down  the letter sequences to use in a variety of experiments.  The draft above was based on the cube of a binomial.  (a + b)³.  When broken down to its most basic form it becomes aaa + aabaabaab + abbabbabb + bbb regroup aaaaa b aa b aa b a bb a bb a bbbbb  (24 units).  I used this sequence as the basis for my twill tie up and then used the sequence again for color in the warp and weft. Once you have pulled the sequences out of Ada's work, you can experiment with a variety of ways to use them.

 

Here is the square of a trinomial represented in a profile draft with colors following the sequence as well.  (a + b + c)²    aa + abab + acac +  bb + bcbc + cc 18 units

 

 

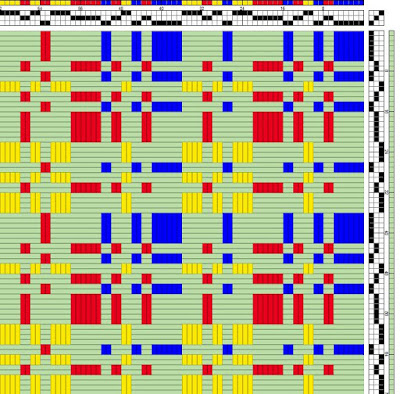
Then, on to Pascal's triangle.  It's fun to google these topics because you come up with  great tutorials for kids (and adults) .  Here is a good one about Pascal's triangle.  I used the fifth row of numbers in Pascal's Triangle for blocks ( 1-4-6-4-1), then mirrored that configuration in the warp.  For the weft, I used the fourth row of numbers (1-3-3-1) and mirrored it as well.  Here is one possible profile draft.  Others can be created by changing the tie-up.

 

These drafts are similar to those built on words.  They are a means to an end and if you don't particularly like what you have created, you can always tweek it to make it more pleasing.  Using this technique for design does help to break down barriers and gets your brain moving in the right direction.  Start with one of these math equations or numerical sequence ideas, expand it  and go from there into something uniquely your own.